Heritage from a distant past
Often the ancient civilisations seem to have had capabilities and knowledge that are difficult to explain on the base of the scientific and technological level of their time, to the point that we are induced to hypothesise that they were inherited from a previous unknown civilisation, which level was much more advanced.
For example the existence of renaissance maps and medieval planispheres (Piri Reis, Oronteus Finnaeus, Mercator etc) with longitude precisions impossible at that time and the representation of Antarctica as it appeared at the end of Pleistocene, was so inexplicable as to force a scientist like Charles Hapgood to postulate the existence, sometime before 8,000 years ago, of an unknown civilisation with the capability of charting the whole world with extreme precision.
But it’s not necessary to look for challenging knowledge and capabilities in order to find evidence of that kind. Also knowledge and figures used today in everyday life can provide straightforward evidence that they have been originated in a very old time by an unknown civilisation, which technological level was much more advanced than that of all known past civilisations.
It’s the case of something apparently insignificant and devoid of any hidden meaning like the actual unit of time: the second. It’s a unit used universally in the world, which characterizes every instant of our life and is fundamental for the description of whatever physical phenomenon. We can hardly underestimate its importance, and yet we ignore what is the origin and the meaning of this unit, that we have inherited with no indication whatsoever about the author, the epoch and the reasons that determined the choice of its magnitude.
The current opinion is that it was originated by the ancient Sumerians because of their sexagesimal accounting system. In fact 86,400 is a number clearly connected to that system, as it can be divided in 24 hours of 60 minutes, each of them made up by 60 seconds. Same origin can be hypothesised for the convention of dividing the circle in 360 degrees, each of 60 minutes of 60 seconds of arch.
The problem is that we don’t have the faintest idea how and why the Sumerian sexagesimal system was originated. It might be, on the contrary, that it was that particular unit of time that originated such out of proportion, almost absurd, accounting system (we could understand much easier the origin of a decimal system for both, the accounting and the division of days and arches).
And in any case, we don’t know what the magnitude of the unit of time represents. Was it a casual choice or instead a length of time with a meaningful connection to some particular astronomical magnitude? And was it invented by the Sumerians or instead the Sumerians inherited it by a previous civilisation, as we did by them ?
The scientific definition of the second
Usually a unit of measure is established on the basis of some significant characteristic of the planet where we live on. For example the unit of length, the meter, has been obtained by dividing the circumference of Earth by 40.000.000, which presupposed a preventive knowledge of its length.
We can reasonably expect that the unit of time, the second, also represents a magnitude somehow related to the length of Earth’s rotation around itself and around the Sun, that is of the solar day and the tropic year. And in fact this is how the modern scientists have intended it and defined it.
The second represents the 86,400th part of the day. Which day? The length of the solar day, that is of the time-span between two successive zenithal passages of the Sun, is not a constant, due to the fact that the Earth’s speed around the sun is constantly changing, because of its elliptic orbit.
The second is a fraction of the “mean” solar day during a whole tropic year. Therefore, in order to establish this’ unit of time it is necessary to know exactly how many solar days are contained in a tropic year. But, again, which year? The ratio between day and year is not a constant, because Earth is continually undergoing a deceleration caused by the braking action of the tides. That’s why modern scientists were forced to chose a particular date to which attach their definition of the unit of time. The definition ratified by the Eleventh General Conference on Weights and Measures in 1960 is: “the ephemeris second is the fraction 1/31,556,925.9747 of the tropic year for 1900 January 0 at12 hours.”
Which means that the length of the tropic year on the 1st of January 1900, at 12 o’clock, had been previously calculated in 365.24219878125 (= 31,556,925.9747 x 86,400) solar days. Usually this number is made round to the fourth decimal as 365.2422 .
However, this is a definition “a posteriori”, and it doesn’t say anything about the real meaning of that unit and which was the reason for the choice of its particular magnitude, which do not seems related in a meaningful way to the length of the year. Whoever established that unit, instead, sometime in a very distant past, had to know a priori the exact number of solar days contained in a tropic year, and he choose its magnitude with the purpose of having a unit with a very significant meaning in relation to both of them.
In other words, the value of the fundamental unit of time, the second, should provide decisive evidence that an unknown global civilisation existed in a distant past, capable of measuring the length of the year with a precision that we have reached only at the end of the 19th century. This can be demonstrated just tracing back the process necessary to establish in a rational way a unit of time derived from the magnitudes that it is supposed to measure, that is the length of the day and the year, in a non-arbitrary or accidental way.
The natural unit of time, U
Let’s see how a unit of time strictly related to both, the mean solar day and the tropic year, should be established in a rational way.
Since man started to solve the problem of measuring the time, he looked at the sky, trying to find out the precise relation between the day and the solar year. This, in fact, is the main problem at the base of every calendar system. Inevitably he discovered that the pace with the sun could be maintained adding one day every four years of 365 days, thus having a year lasting exactly 365.25 days. This is called the “Julian year”, because it was introduced in the present calendar by Jules Caesar, on 44 b.C.
The Julian year is 0.0078 days longer than the actual length of the year, assuming as precise, as we said, the length of 365.2422 days. So, after 1/0.0078 = 128.205 years we have a full day in excess. Therefore the most precise possible calendar could be obtained adding one day every four years of 365 day, except on the 128th, thus establishing a cycle of 128 years. (We should remind that the cycle of 128 years was discovered by the Russian astronomer Glasenapp at the end of the 19th century, when the technological and scientific progress allowed to measuring the length of the year with a precision up to the fourth decimal. He proposed to revise the Gregorian calendar accordingly, but without success) .
Now, in a cycle of 128 years we have: 128 x 365.2422 = 46751.0016 days. With a calendar based on this cycle we would have an average “error” of 0.0016/128 = 0.0000125 = 1/80,000 days per year. This fraction is the natural candidate to become our unit of time.
As 1/0.0016 = 625, assuming that the ratio between the solar day and the tropic year would be constant (which actually is not), we would have a full day in excess only after 625 x 128 = 80.000 years. In theory, then, if we add one day at the end of the 625th period of 128 years, we could have a cycle of 80,000 years with a nil average error per year. It’s impossible to imagine a more precise calendar.
Therefore it looks spontaneous and quite logical to define the “natural unit of time” as the fraction U = 0.0000125 of the average solar day (for a year of exactly 365.2422 days), which contains exactly 80,000 of these units.
80,000 is a round figure very convenient for the division of the day in identical parts, each with the same number of units U and identical subdivisions, down to the unit U. For example 10 hours of 8,000 units each and subdivisions of 400 and 20 units, as 8,000 =203. From this an accounting system on base 20 could spontaneously derive, which would impact also on the structure of the calendar, with the division of the year in months of 20 days each and so on. Precisely as in the accounting systems and the calendars of Central America.
Of course the fact that the mean solar day contains exactly 80,000 natural units, U, is only an accidental chance. What cannot be considered accidental, however, is the way that led to find out the magnitude of this unit, because it presupposes a precise knowledge of the length of the tropic year. And definitely it cannot be considered accidental the transformation of the natural unit U in a more manageable unit of time, by means of a precise multiplier.
The fundamental unit of time, the second
The most important property of a unit of measure is its ability to be used as a multiple and sub multiple of magnitudes of different size. The unit U which divides the solar day in 80,000 parts is convenient, but not the best possible, because this number is divisible only by 2 and 5. A number divisible also by 3, could be more flexible and useful.
This can be achieved very easily by dividing the natural unit U by 1.08, thus establishing a new unit of time which value is S = U / 1.08. In this way the mean solar day is divided in 80,000 x 1.08 = 86,400 parts, a number more convenient for measuring parts of days and years.
We therefore define the “second, S,” as the fraction 1/1.08 of the natural unit of time U.
To conclude, the second is not a span of time established by chance, but it’s a magnitude with a very precise relation with the length of the average solar day and the astronomical cycle of 128 years. We can prove, in fact, that the multiplier 1.08, which transforms the natural unit in a second, far from being casual, is the result of a precise choice made sometime in a distant past, in order to render more practical and flexible the division of the day and the structure of the calendar.
Epoch when the second was established
It’s important to note that the natural unit of time, U, was not established on the basis of the number of full days contained in a cycle of 128 years (46751, a figure that in theory an ancient civilisation could have found out just counting the days between the solstices for a time long enough), but only on the basis of the excess of 0.0016 days in a period of 128 years, 0,0000125 per year, that is 1/80.000 days, a precision impossible to achieve without technologies and scientific knowledge comparable to those reached by our civilisation at the end of the 19th century.
One might object that the figure 0.0016 is the result of an approximation of the length of the tropic year to the fourth decimal, a choice that could be deemed arbitrary. The length of the tropic year, as we said, has been measured, for the 1st January 1.900 at 12 o’clock, in 365,24219878125 days, that is 0,1053 seconds shorter than the one considered in order to obtain our units of time.
The modern scientists were forced to fix the length of the year for a very precise date, because this magnitude decreases gradually, as we said, due to the braking action of the tides and to other not well known factors. On the basis of ancient observations of solar eclipses, it was possible to calculate the average deceleration of Earth in about 1.4 milliseconds per century. A simple operation allows us to calculate that the length of the tropic year was exactly 365.2422 solar days about 7,500 years ago.
A civilisation able to measure the length of the year with absolute precision around that date, would have found precisely that number and therefore would have had a strong indication and motivation to establish the natural unit of time. This, although not a proper evidence, is in any case consistent with the asserted ancient origin of that unit.
We can conclude with a high degree of confidence that the actual unit of time, the second, is the result of a precise choice made by a civilisation able to calculate with great precision the length of the tropic year. An unknown civilisation from which all the ancient civilisations have been originated, or at least influenced. Clear evidence of this is provided by mythological figures and sacred numbers left by the latter all over the world.
Sacred and mythological numbers of ancient civilisations
The introduction of the “second” establishes a cycle of 86,400 years strictly connected to the natural cycle of 80,000. Both of them contain a round number of cycles of 128 years, and all the magnitudes characteristic of one of them can be transformed in equivalent magnitudes of the other through the multiplier 1.08.
They are perfectly equivalent, but they give origin to very different structures of the calendar and different accounting systems. In one case an accounting system on base 20, a division of the year in months of 20 days and so on are promoted ; on the other an accounting system on base 60 and subsequent divisions of the day and the year.
Both figures, 80,000 and 86,400, with their multiplier 1.08, can be expressed in forms of extreme elegance, which make them very intriguing and significant from a mathematic and numerical point of view,
80,000 = 128 x 625 = 1,600 x 50 = 27 x 54
86,400 = 80,000 x 1.08 = 128 x 675 = 1,600 x 54 = 27 x 33 x 52
675 = 625 x 1.08 = 54 x 1,08 = 33 x 52
and so on, forming a very impressive set of numbers.
The probability that all of this could be the result of a fortuitous coincidence is almost nil.
Whoever is familiar with ancient calendars and accounting systems and with sacred numbers e mythological figures, would realize that numbers like 80,000, 86,400, 1.08 and their multiples and submultiples, represent the mathematic and astronomical knowledge and the mythological numerology of the whole ancient world, both on one side and the other of the Atlantic. In two well characterised areas: America belongs to the area of the natural unit of time, U, having adopted a calendar and an accounting system entirely based on number 20. Europe and Asia, instead, belong to the area of the second. Evidence of this is provided by an impressive complex of figures handed down by ancient civilisations, several of which still in use today (just for example, the division of the day and of the circle).
In particular 108 and its multiples and submultiples (54, 216, 432 and so on) appear to be figures endowed with an undoubtedly sacred meaning, although nobody, so far, was able to explain in a convincing way the reason of it. We can find them from one side to the other of the Eurasia continent and in the most disparate situations.
They are the most common figures in the sacred architecture. For example the temple of Angkor Vat, in Cambodia, has 54 towers, 108 statues along the entrance alleyway, 540 effigies of the gods Deva and Asura and so on; the temple of Baalbek, in Phoenicia, had 54 columns; in the holy town of Lasha, Tibet, there were 108 temples; 108 were the chapels of the Padmasambhava temple; and so on. They are also recurrent figures in ancient literature: the Sumerian king Enlil presented Aadamu with 108 perfumes; king Gudea employed 216,000 workers to build the temple of Ningirsu; he used to offer his guests 108 different kinds of food; and so on.
And they are omnipresent in a long series of cosmic cycles, mythologies, religions and so on: the Indian cycle called Manvantara is made up by 64,800 (108 x 600) years; the Kalga cycle, also Indian, lasts 4,320 (108 x 40) milions of years; the time span of the antediluvian reign in the Babylonian mythology is made by 432,000 years; 108,000 in the Sumerian one; the Buddhist and Hindu rosary is made by 108 pearls; the Catholic rosary is made by 54 pearls (plus 5 outside the ring); the sacred Tibetan books of Khagiur are made up by 108 volumes; the Rig Veda have 10,800 verses, each with 40 sillabes, for a total number of 432,000; the Valhalla of northern mythologies had 540 doors, and from each of them 800 warriors got out, for a total of 432,000. And so on (this list has been taken from a book of Prof. Emilio Spedicato, who makes a long inventory of such figures all over the world).
All these figures are related to the 128 years cycle through the units of time established on its base. It was a secret knowledge transmitted in ancient societies amongst the priestly class, which had the task to measure the time. Whoever controls the calendar, in effect, controls the society. It was a tradition still alive 2,500 years ago. As a demonstration we can quote such an authoritative and well known source like the Bible. In Numbers 31, 32-47 we read:
“The spoils, the remainder of the booty captured by the soldiers, came to 675,000 sheep and goats, 72,000 head of cattle, 61,000 donkeys, and in persons, women who had never slept with a man, 32,000. Half was assigned to those who had taken part in the war, namely 337,500 sheep and goats, of which Yahweh’s portion was 675; 36,000 head of cattle, of which Yahweh’s portion was 72; 30,500 donkeys, of which Yahweh’s portion was 61, and 16,000 persons, of which Yahweh’s portion was 32. … As for the half coming to the Israelites … this came to 337,500 sheep and goats, 36,000 head of cattle, 30,500 donkeys and 16,000 persons. From this half, Moses took one out of every 50 …”
Figures like 360 and 72 are clearly derived from the solar calendar and we find them in all cultures of the world. But their connection with the 128 years cycle is not immediately evident. Numbers like 32 (=128/4) and 675 (= 86.400/128), instead, are strictly related to the 128 years cycle. Even numbers like 61, 30.500 and 50, apparently not belonging to it, appear to be instrumental for determining figures associated with that calendar. For example:
30.500 + 16.000 +72 + 61 + 50 + 36 + 32 = 46751, which is exactly the number of entire days contained in 128 years (128 x 365.2422 = 46751.0016).
Mere coincidence? Could be, but the odds are against this conclusion. The ancient Jewish priest who wrote these verses, probably in the Babylon of 2,500 years ago, knew the calendar based on the 128 years cycle and utilised this passage of the Bible as a “reminder”; probably encrypted in the text there are other information related to this calendar and its employ.
This simple quotation from the Bible, under everybody’s eyes, represents definitive evidence that ancient priests had scientific knowledge higher than those that we think possible for their epoch, which were kept secret, and that’s why they got lost. Hints of them, however, have survived everywhere as figures that clearly betray their origin, down to the present civilisation, where they play a fundamental role in all the sciences and applications that make use of the unit of time, the second, and the units of trigonometry.
We can exclude that they were the product of ancient populations known to us, because they didn’t have the technical means and scientific knowledge to do it. In order to establish the units of time and all the magnitudes connected to them, they should have known the length of the year with a precision up to the fourth decimal, and from that knowledge to establish the 128 cycle, which we didn’t know before the 19th century.
(The present civilian calendar, inherited by the Romans and fixed by pope Gregory XIII on 1582, is definitely not the most rational and even less the most precise of possible calendars. It only takes about 3,300 years for this calendar to accumulate a difference of one day with respect to the solar year. This time-span could be increased to 80,000 years if we adopted a calendar based on a cycle of 128 years, as it was proposed by the Russian astronomer Glasenapp at the end of the 19th century).
We can therefore take for certain that such an insignificant magnitude like the second, apparently with no hidden meaning, is by itself living evidence that in a distant past a primeval civilisation existed, with a technological and scientific level as to allow very precise astronomical measurements and complex mathematical calculations. A civilisation which is at the origin of (or at least had influenced) both, Eurasiatic and American known ancient civilisations.
THE ROOTS OF MESOAMERICAN CIVILISATION
THE CALENDAR OF CENTRAL AMERICA
The evidence that we find in the calendars and the accounting systems of Central America is no less important than that of Eurasia, with a fundamental difference: they clearly derive from the natural unit of time, U, which is the 80.000th part of the day.
Aztecs, Mayas, Toltechs, and Olmechs before them, had in common an accounting system on base 20 and a calendar based on an auxiliary year of 260 days (called “Tzolkin” by the Mayas), divided in 20 weeks of 13 days, and on an auxiliary century of 52 years. The solar year was divided in 18 months of 20 days each, for a total of 360 days, to which they added 5 final days considered inauspicious and therefore “non-existent”.
Extraordinary importance was given to all combinations of numbers derived from the intertwine of the solar year with the auxiliary year, inside a period of 52 years. For example:
365 x 52 = 260 x 73;
360 x 52 = 260 x 72 ;
360 x 13 = 260 x 18
and so on in an extraordinary intertwine that deeply impressed the modern scholars who studied it.
This calendar played a fundamental role in central American societies, regulating their existence day by day in a overwhelming way (as today’s calendars, to be objective). Obviously it exerted a strong fascination upon generations of scholars, who dedicated hundred of books to its description. Several attempts have been made to explain the origin of this numerical system and of this calendar, most of which awkward and improbable.
A simple and immediate explanation is that they inherited them by the same previous civilisation, which had established the natural unit of time, U, and a calendar based on the 128 years cycle (we have to remember that 1/80,000 days is exactly the average error per year during such a cycle).
The fact that the cycle last 128 years is a lucky coincidence. 128 equals 27, which allows us to make all families of perpetual calendars, all with the same average precision.
The procedure is the following:
1) We compute the time in weeks of n days each and years of 365 solar days.
2) At the end of a period S = 4n years (which we will call auxiliary century from now on) we add n days
3) At the end of a period of C = 128n years, that is 32 S, the n days are NOT added.
Whatever the value of n, at the end of a cycle of n.128 years we would have the same astronomical situation that we had at the beginning (if it was a solstice it would be again a solstice). Besides every cycle C will have a round number of weeks and years.
A small inconvenient of this (and whatever other) calendar is that the solar year cannot contain a round number of weeks (unless we put n=1). Easy to remedy by adopting, besides an auxiliary century, also an “auxiliary year”, T, with a round number of weeks and a fixed ratio with the solar year within an auxiliary century.
If we adopted the natural unit of time, U, the most natural choice should be that of dividing the year in 18 months of 20 days each, plus 5 final days, and adopting an auxiliary year of 20 weeks of n days each. We would have, therefore, a family of 18 calendars, summarised in the following chart, all with the same properties and characteristics:
|
n (days) length of the week |
T = 20 n (days) length of the auxiliary year |
S = 4 n (solar years) length of the auxiliary century |
C = 128 n (solar years) length of a complete cycle |
|
1 |
20 |
4 |
128 |
|
2 |
40 |
8 |
256 |
|
3 |
60 |
12 |
384 |
|
4 |
80 |
16 |
512 |
|
5 |
100 |
20 |
640 |
|
6 |
120 |
24 |
768 |
|
7 |
140 |
28 |
896 |
|
8 |
160 |
32 |
1024 |
|
9 |
180 |
36 |
1152 |
|
10 |
200 |
40 |
1280 |
|
11 |
220 |
44 |
1408 |
|
12 |
240 |
48 |
1436 |
|
13 |
260 |
52 |
1664 |
|
14 |
280 |
56 |
1792 |
|
15 |
300 |
60 |
1920 |
|
16 |
320 |
64 |
2048 |
|
17 |
340 |
68 |
2176 |
|
18 |
360 |
72 |
2304 |
The following relations exist between the solar and the auxiliary year:
1) 360 x 4n = T x 72
2) 72T + (5x4n) +n = (72+1)T + n = 1461 n = (360 + 5) 4n + n
Relation 2) expresses the number of days and weeks of each auxiliary cycle (with the exception of the 32nd , which is one week shorter).
1,461 is known as the “sothic” number (from the Egyptian sothic period of 1461 years). It is the number of days in 4 Julian years (365.25 x 4= 1461) and represents a recurring figure in this family of calendars; an auxiliary cycle contains 1461weeks and 20 auxiliary centuries contain 1461 auxiliary years.
A complete cycle of 128 n years contains (1,461x32)-1 = 46,751 weeks, which is another characteristic figure of these calendars, because it’s the number of solar days contained in 128 tropic years.
It’s quite evident that the central America’s calendar belongs to the family of calendars described on the above chart, precisely that with a week of 13 days. Whatever other length of the week would give place to a perfectly similar calendar, with exactly the same “magic” intertwine of numbers, due to relations 1) and 2), and with the same characteristic figures.
The perennial astronomical clock
It remains to understand, now, why an advanced civilisation should have invented a calendar apparently so complicated. In reality it’s quite simple and rational.
This family of calendars is very interesting not only for the elegance of its structure, the impressive intertwine of numbers and the many possibilities that it offers, but also for the fact that it is characterised by a week which rolls indefinitely and is a sub multiple of both, the auxiliary year and the auxiliary century. The solar year and the auxiliary year are in their turn submultiples of the auxiliary century. Therefore there are precise relations between all of these units.
This allows to make an astronomical “clock”, valid for whatever length of the week, easy to use, and capable of keeping indefinitely the synchronism with the solar year. Not only: the same clock is a sort of perennial almanac, that keeps under control and represents in a very compact way all the astronomical magnitudes of some interest, from the hour of dawn and sunset, to the count of days, weeks and years, solar and lunar eclipses, movement of planets and constellations of the zodiac and so on.
Clock-almanacs of this type, in fact, have been carved on the stone several times in pre-Columbian Mexico. In all likelihood they reproduce the front side of some mechanical devices, kept with the utmost care as sacred objects by the priestly class.
Of course this is only an hypothesis, as there is no information about the finding of one of such devices (which is most improbable, because either they were hidden in very secret caches, either they were destroyed by the Spanish), that could prove beyond doubt this claim. But it can reach a very high degree of likelihood as we go through the process of making a clock based on this family of calendars.
The solar day
The basic mechanism is made up by a central disc, which represents the “sun”, that is a solar day, with (at least) one hand that makes a complete turn in one day. Something similar to a modern clock, with hands that measure hours, minutes and seconds. With an important difference, however. In most central America’s representations this central disc is divided in two parts by an horizontal line, which “obscures” the upper side of the disc (see following pictures).
The meaning of that line looks clear. The today’s almanacs report for each day the hours of the dawn and of the sunset for a certain latitude and longitude. It’s an information of great interest in everyday life, but none of the modern clock is able to provide it. And yet it’s very simple to do it and very practical.
Let’s see how. We divide the clock-face in 24 hours instead of 12. We fix a reference latitude and longitude. In this way a simple horizontal line will indicate the hour of the dawn (on the right) and that of the sunset (on the left), for that particular latitude and longitude. On the upper side of the line it’s night, on the lower day light.

An ad hoc algorithm will move day by day the line up or down, according to the season, so as to maintain the synchronism with dawns and sunsets.
It’s an extremely simple mechanism which would allow us to know day by day, with just a look, everything about the movements of the sun and the hours of darkness and light. Information that today is provided only by very detailed almanacs.
The auxiliary year (tzolkin)
The clock is based on relations 1) and 2) and therefore there is little choice on how it can be realised. The basic mechanism is made of the central wheel which counts the hours of the day and night. An outer ring counts the days of the week, completing a full turn every week. The number of partitions of this ring varies according to the length of the week selected with an ad hoc regulation. The same clock, in fact, works properly for whatever length of the week. (As the length of the week can be changed, a counter placed on a window of the central wheel could be more practical than an ad hoc ring).
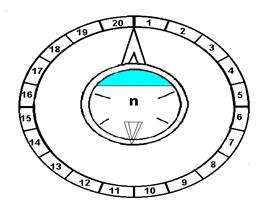
What does not change is the ring outside, divided in 20 parts, along which move two hands, one long and one short. The long hand counts the days and moves forward one step every solar day. The short hand counts the weeks and moves forward one notch every time the inner wheel completes one week.
A complete revolution of the long hand equals 1 months of 20 days.
A complete revolution of the short hand equals 20 weeks of n days, that is 1 auxiliary year (T=20n).
Due to relations 1) and 2):
- the long hand completes 73 (72+1) revolutions every 4 years of 365 days.
- the short hand completes 73 (72+1) revolutions every auxiliary century, that is 4n years of 365 days.
At the end of the auxiliary century the two hands will be aligned on the zero, having the long hand made n more revolutions than the short hand. At this point, in order to re-phase the calendar with the solar year, n days, that is one week, must be added. This can be achieved in different ways; for example by stopping the hands for one week and rotating counter-clock-wise the ring of the 20 days. The new auxiliary century therefore begins with both hands on box n of the ring which becomes the new reference zero.
(In this way 20 successive auxiliary centuries would be characterised by a different initial day, and each year of the n groups of 4 years of the century would begin always with the same day. So each one of the 20 centuries would be characterised by a different group of four days, which begins in turn every group of four years. It’s only one of the many interesting characteristics and possibilities offered by this calendar).
The same operation is repeated for 31 auxiliary centuries (of 4n solar years each). At the end of the 32nd the mechanism will restart a new complete cycle of 32 auxiliary centuries, without the addition of the usual extra week. And so on indefinitely. At the end of every cycle we would have the same astronomical situation with regard to the sun.
The Counters
It is a simple mechanism, which provides directly all the magnitudes necessary to keep under control the flow of time:
- number of hours and days
- number of months of 20 days (revolutions of the long hand )
- number of auxiliary years of 20 weeks (revolutions of the short hand)
With these elements we can, by means of ad hoc counters, visualize all the information of some interest in a calendar.
Let’s see what they could be.
First, the actual date, that is the day of the month in the solar year and the day of the auxiliary year. They could be shown at the sides of the central mechanism on four small windows, two for the solar date, two for the auxiliary date.
Then we have to position these dates in the calendar, counting the time elapsed since a starting date. Due to the use of an auxiliary year it becomes natural to first positioning the day inside the auxiliary century of 4 n auxiliary years. This inevitably is obtained by partitioning that period in smaller periods. For example, in today’s civil calendar we often add to the actual date the progressive number of the day and of the week, and we divide the year in quarters and so on.
Same divisions can be done in a much more rational way in this new calendar, descending from the relations existing inside an auxiliary cycle. An elegant division is prompted by the fact that 4 solar years contains exactly 72 + 1 months of 20 days (72 months of 20 days + 4 of 5 days). 72 can be divided in many ways, for example by 4, 3 and 6, that is each of the four solar years could be divided in three semesters. The counter therefore would show the number of the solar year in the bunch of four, then the number of the semester in the year (1-3) and finally the number of the month within the semester (1-6). Finally there should be an indication positioning the group of four years within the auxiliary century (1, 2 ...n). In this way our day is positioned precisely with respect to the solar year within the auxiliary century .
Then we should position our day with respect to the auxiliary century, what can be done with a counter identical to the first one, due to the fact that 1 auxiliary century is made up by 72 + 1 auxiliary years.
The same counters can be utilised to count the number of the day within a group of four years, and the number of the week within the auxiliary cycle, due to the fact that four years contain exactly 1,460 days ((72+1).5.4) and one auxiliary cycle 1,460 weeks (plus one only at the end, in order to maintain the coincidence with the sun).
Our counters would look more or less like the following.
There is another information that is required from a “general purpose” calendar, that is the precise number of days elapsed since a starting date. This information is not really useful in everyday life, but it is essential for astronomers, historians and archaeologists. The instrument in use today for this purpose was provided by the French philosopher J. Juste Scaliger who on 1583 published the book “Opus Novum de emendatione temporum”, in which he established a “universal” calendar based on the account of solar days since a particular date, which he chose to be the 1st of January - 4712 (Julian year) at midday.
This calendar is currently used by astronomers and historians to establish and compare the date of astronomical events (like eclipses, conjunctions etc) and historical events, comparing different calendrical systems. For example the Thompson correlation and all the others related to the starting day of the Mayan calendar are based on Scaliger’s universal calendar.
The simplest way to count the days is through a series of registers connected to the long hand, which moves one position every day (from 1 to 20). A first register counts the complete revolutions of the hand from 1 to 18 (this number should be 20, but in this example we follow the same system of the Mayas), that is one year of 360 days. Once completed it starts again, while giving an input to the successive register, which counts from 1 to 20 years, for a total of 7.200 days. Its output goes to a third register, which counts 20 times the previous one, for a total of 144.000 days; and finally we have a register that counts n times the content of the previous one, completing a long cycle.
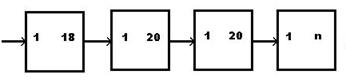
The total number of days elapsed since the start of the calendar is given simply by adding the content of each of the four registers and the number indicated by the long hand.
In this way the calendar provides a “short” count which gives the days, weeks, months and years within the auxiliary century (called by the Mayas the “calendar round”) and regulates the entire life of the society, and a “long” count which gives the total number of days elapsed since the beginning date.
The “long” count would divide the calendar in n periods of 400 years (of 360 days), each of them composed by 20 groups of 20 years and so on. A date of this calendar should report the day and month of the solar and auxiliary years, together with the total number of days elapsed since the beginning, reported as the content of the different counters, exactly as in the following Mayan dates:
8 . 14 . 3 . 1 . 12 1 Eb 0 Yaxkin,
8. 11. 7. 13. 5 3 Chicchan 8 Kankin
The first date identifies the 1,253,912nd day of the calendar (8 baktuns, 14 katuns, 3 tuns, 1 month and 12 days) and its solar and auxiliary dates. The second identifies the 1,233,885th day (8x144,000 + 11x7,200 + 7x360 + 13x20 + 5) and so on.
The central mechanism of our clock-calendar would therefore look more or less like the following:
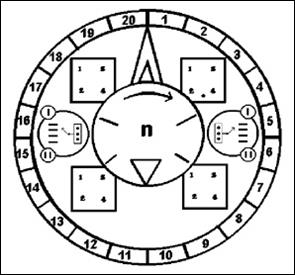
In no way this is intended to be an interpretation of the precise meaning of the corresponding counters of the Aztec calendars. It’s just an example to show what kind of information could be represented in the central mechanism of a calendar of this type and how it could be organised. Several representations of this mechanism have been found in Mexico and all of them show the same basic scheme; they should provide the same information about the solar and auxiliary years, although represented in different styles.
 Sun Stone
Sun Stone 


 Teocalli
Teocalli

Other astronomical magnitudes
In our almanacs an information that is always represented is the phase of the lunar cycle, or month, with all what is related to it, that is solar and lunar eclipses.
Other elements are the movements of the sun in the zodiac, that is the signs of the zodiac, the movement of the planets and their synodic years, prevision of conjunctions, eclipses etc. All these information should be represented in our astronomical clock, so that we can have a complete vision of what is going on in the sky every day, and make prevision of future astronomical phenomena.
This information can be represented on external rings and windows around the central mechanism, that visualise astronomic and astrological phenomena and cycles which have a constant ratio with the solar or auxiliary years, like the position of the sun in the zodiac, the lunar cycles, the synodic years of the planets and so on. The precession too can be monitorized, through a slow shift of the zodiac.
All of these magnitudes are independent from the length of the week, which however is the most important element in a calendar, because it has a major impact on the life of a society and determines the length of the auxiliary year and the auxiliary century (for example, a week of 8 days would determine an auxiliary year of 160 days and an auxiliary century of 32 years, instead of 260 days and 52 years for a week of 13 days).
The length of the week can be set and changed through an ad hoc regulator, so there must be on the clock the clear indication of the selected length of the week. The final aspect of our astronomical clock could therefore be the following.
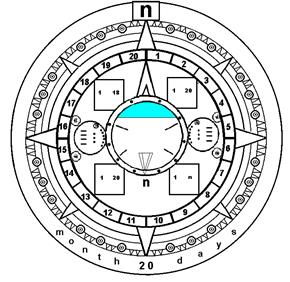
Central American calendars
The aim of this long description is not to suggest a change to the civil calendar (unthinkable today), but to demonstrate the rational of the calendar used by Central American civilizations, Aztechs, Mayas, Toltechs, and Olmechs before them. It was a calendar based on an auxiliary year of 260 days, divided in 13 months of 20 days (or in 20 weeks of 13 days), and on a century of 52 years. The solar year was in its turn divided in 18 months of 20 days + 5 end days.
It is evident that this calendar belongs to the family of calendars described above. We don’t know what determined the choice of 13 as the length of the week. A likely reason could be that the auxiliary year of 260 days is well suited to keep under control some astronomical magnitudes, like for example the synodic year of Mars, which is exactly 260 x 3 = 780 days. The synodic year of Venus too, 584 days, has a round ratio with the solar and auxiliary years, as 584x65=260x146=365x104, (where 65 = 260/4). As a matter of fact, the central American civilisations gave an enormous importance to the synodic year of the planets, in particular Venus and Mars. Another reason why Venus was regarded as a very special planet could be the fact that 365/584=0,625= 80/128 , which is a quite extraordinary coincidence.
A possible objection is that, according to most chronicles about that calendar (but not to all of them), they did not have leap years. Most likely they added an entire week only at the end of every auxiliary cycle, as required by this type of calendar. They had the means to establish with precision the dates of solstices, which is proven by the extremely accurate alignments and the existence of gnomons in their temples. It’s not likely that they ignored the shift of the solar year with respect to their calendar and didn’t correct it.
At the end of each auxiliary century of 52 years, there was a delay of 13 days, that is exactly one week. These 13 days, added to the final unlucky 5 days of the year, formed an additional month of 18 days (like the number of the months in a solar year), which ended the cycle under the aegis of terror and death. It was the month during which, according to the traditions, the end of the world was expected. To avert this danger, the Aztec priests accomplished terrific slaughters. Thousands of prisoners were sacrificed, while the population remained barricaded in their houses, prey of terror. Those days were so inauspicious, that they were never named, neither accounted for: they didn’t exist. No wonder that the chronicles of that period do not mention them.
Also the 5 days of the additional month at the end of each year, that was called by the Mayas “uayeb” (nameless), of which it was never found a representation, were considered non-existent. This is why the solar year was considered of 360 days.
There have been several attempts to explain the origin of such extraordinary calendar. But so far nobody succeeded in providing a likely explanation or finding out when and where it appeared for the first time. The only certitude is that it is very ancient and was used by the most ancient known civilisation of Central America. There is no trace witnessing a gradual evolution from a more simple structure, like, for example in the Roman calendar. It starts from the beginning in its full capacity. On the contrary it seems that the capacity to exploit all its initial characteristics and potentiality was gradually lost.
For example, it was easy, even if there was a loss of knowledge, to maintain the right way of keeping the record of the “short” count, that is within an auxiliary century of 52 years. But the characteristics of the calendar after that date where lost very easily, due to the long time span between one operation and the following. There are clear signs of this loss of knowledge amongst the Mayas, but it’s too long to discuss this matter in this article.
Who originated the central American calendar
It’s quite evident that this calendar is based on the 128 years cycle and derived from the natural unit of time, U, which is the 80.000th part of a mean solar day. We have to assume therefore, that it was designed by the same people who found out that unit of time. People belonging to a civilisation advanced enough to measure the exact length of the synodic year, what could have been done only with instruments of high technology.
Therefore they were certainly able to make astronomical clocks the type so far described. For some reason this unknown civilisation has disappeared, but either directly or through survivors, it transmitted its astronomical knowledge to the populations that started the ancient known civilisations.
We have to assume that the natural unit of time, U, and the second, were established by the same civilisation, or at least by two populations, developed in the same cradle and belonging to the same cultural horizon, who wanted to differentiate from each other by means of two different calendrical and numerical systems.
Evidently there had been immigrants or survivors, belonging to the area of the natural unit of time, that landed on the coasts of central America, thus originating the civilizations of that area. They must have had with them several astronomical clocks, of different complexity, from those very simple, providing only essential information in a plain way, to the most elaborated and artistic objects, with all possible astronomic information.
They had to be kept with the utmost care, but soon or later they had to stop working and most of them went rotten. But the more beautiful were regarded as sacred object and kept with extreme care and jealousness during a span time of several millennia. They were reproduced on the most important sites of the society, like the altars of the temples and the thrones of the kings.
That’s why we have accurate images of them. Probably the carvers did not know any more what was the meaning of the objects they were reproducing on the stone, and they did not understand the nature of many of the indications of the object, either because it was corroded by time, either because they had never seen anything alike. In any case we have several representations of clocks of that type. Some are very simple and linear, others are astonishingly elaborated. All of them, however, have the same basic structure. They all reproduce objects of the same category, with similar functions: clock calendars.
The Teocally’s calendar
One of the best kept and represented is the calendar carved on a throne of the Teocally temple in Tenochtitlan. The central mechanism is quite schematic, with no representations of gods or animals. We clearly recognize the central clock, which indicates the day’s hours, divided in day and night by a horizontal line. Outside there are two rings, one indicating the week, the other the 20 days month. And then the counters and registers organised exactly as in our example and in the large stone calendar that we’ll see later. The outer rings represent astronomical cycles that we can only guess, surely connected with the moon, planets and zodiac.


The carver that made this sculpture was copying a real object, not just representing an abstract concept.
Objects of the same kind were reproduced in several places (the essential part being the central clock with its counters).




All of them present the same basic design of the central mechanism. They had to provide the same information.
The Aztec Sun Stone
The most beautiful, elaborated, complete and artistic representation of an astronomical clock was carved by the Aztecs a few years before the arrival of the Spaniards, discovered only on December 1790, buried in the "Zocalo" (the main square) of Mexico city.
It is known as the Aztec Calendar, or the Sun Stone, a huge monolith, with a diameter of 12 feet, a thickness of 3 feet and a weigh of 25 tons, an amazing indication of the importance of the object that it was intended to reproduce.
 The Sun Stone
The Sun Stone
First, we note, at the top of the disk, in all evidence, the number 13, that establishes the length of the week and, as a consequence, the length of the auxiliary year (called Tzolkin by the Mayas). In the middle it’s clearly recognisable the mechanism of the astronomical clock, with the “god” sun right in the centre, representing the hours of the solar day and the days of the week. Two hands, long and short, point to a first external ring, divided in 20 section, one for each day of the month of the auxiliary year. Around the central clock there are counters and registers that show the relevant information about the actual date in the short and long count. Outside the ring with the 20 days of the month there is another ring divided in 40 rectangles, each with 5 units inside. We have therefore 200 units, that might represent the 200 synodic years of Mars contained in 600 auxiliary years of 260 days.
The successive ring is divided in 8 sectors, each containing 10 divisions. It might indicate the 80,000 years of a great cycle (128 x 625), or the 80 synodic years of Venus contained in a cycle of 128 solar years or some other astronomical magnitude of some interest. For example, if we suppose that the ring represents a cycle of 1664 (32 x 52) years, each of the 80 divisions represents a period of 20,8 years, that is exactly 13 synodic years of Venus, a figure quite significant, coincident with the “scale” of this calendar.
The successive ring is divided in 32 sector and the final one in 64, both numbers related to the 128 years cycle. Very interesting is the symbol that appear six time on the external ring, a sort of rectangle with five units inside and 3 notches on top. It might represent magnitudes related to the lunar cycles, like for example the 3 x 33 lunar months and 5 Venus’ years contained in 8 solar years.
Then there are 12 animal-like figures, that could represent the 12 signs of the zodiac. The final band contains 20 sections, each with 5 notches ; possibly some magnitude related to the long count.
Of course, these are only wild guess, or better simple examples of which could be the information provided by the various sections of the clock. Most probably even the Aztec priests were no more able to interpret all of its details. In any case it is quite likely that the Aztec carver had faithfully reproduced, almost like in a picture, a real mechanic object, to the point that we could make an astronomical clock perfectly functional, identical to the representation of the Sun Stone. All we have to do is deciding what information we want to provide in its various windows and rings.
The mark of Atlantis
The Sun Stone in all likelihood is the reproduction of a mechanical device, a sort of astronomical clock, capable of measuring the time according to a calendar based on the 128 years cycle and the natural unit of time U.
It provides additional evidence of the existence of that unknown civilisation, prior to the Central American civilisations, which possessed advanced astronomical and mathematical knowledge, and the technology necessary to make a mechanical device of that type.
A question then immediately arises: “Where and when did this civilisation exist?”.
Let’s assume that the “Sun Stone” really reproduces a mechanical clock. Usually on objects of this kind there is a signature, or a label or a trademark, which identifies the author and/or the country where they come from. Something of this kind could be represented in the lower part of the “Sun Stone”, where a scene is illustrated that is not functional in the mechanism of the clock and looks rather strange.

The conventional interpretation of this image is that it represents two “feathered serpents”, swallowing two men. There are, however, a number of details in it, which do not make sense in this perspective. It appears that the Aztec carver could not understand what was represented in the model he was copying from, and therefore he introduced some small modifications in order to have a representation that made sense to him. If we could find out how his model looked like, we might have indications about the origin of the mechanical device represented in the Sun Stone.
We can solve the problem by examining the image piece by piece, beginning with the two human figures. If we isolate them from the rest of the representation, we obtain an image clearly defined, that in itself makes complete sense.

It represents two persons with some very significant attributes, which characterise them as two “gods”. Their earrings, or better “ear-plates”, for instance, are a typical attribute of the “gods” through all Central America (note that even the sun-god at the centre of the stone has earrings of the same type), India, China and South East Asia. Even their “headgear”, is typical of the “gods” in the same areas.
The subject is clear and consistent, and therefore we can assume that for this part no significant modifications, with respect to his model, have been introduced by the carver. If there are modifications, then, they should have been introduced on the remaining part of the representation.

Examining the figure above, we immediately identify a first probable modification in the “hats” of the two presumed serpents. It looks likely that in the original model they had a symmetrical shape, and that one of their extremities was slightly modified in order to represent the “nostrils” of the two monsters. A second obvious modification, then, had to be done in order to give them eyes. If we reinstate the original shape of the hats and we cancel the eyes, we obtain an image that should be very close to that of the original model .

The new image is clear, consistent and makes perfect sense to us. Instead of two unlikely “serpents” swallowing two men, it represents two perfectly recognisable elephants, with their trunks raised, behind two “gods”. This image, however, could not make sense to an Aztec, who did not know anything like an elephant. Therefore, he had to change a few details in his model, in order to represent something that made sense to him.
A “trademark” representing two gods and two elephants on the back, where could it come from? The first answer that comes to mind is Southeast Asia, India or Indo-China. The Indian civilisation had advanced knowledge both in the astronomic and mathematic fields, was perfectly able to make complicated mechanical devices and has produced sacred numbers which undoubtedly derive from the 128 years cycle. But we don’t have any evidence that it was able to make mechanisms of such complexity, neither that it had designed a calendar like the Central America’s, based on the natural unit of time and on a vigesimal accounting system. Besides, there is no evidence at all that about prehistoric contacts between India and America.
India, however, was not the only place where elephants, the type represented on the Sun Stone, existed. It’s a well known fact, even if almost always overlooked, that elephants existed in South America until the end of Pleistocene, about 11.500 years ago. They were not mammoths, which populated North America, Asia and Europe. They were proper elephants, similar to the Asiatic type, from which, however, scientists are keen to distinguish them, by naming them “mastodons” (mastodons lived in North Africa and got extinguished millions of years ago). Nobody knows when and from where they came to South America, where their bones can be found in many places, often in relation with man, like in the famous archaeological site of Monte Verde, in Chile, which inhabitants lived around 12.500 years ago hunting elephants.
Elephants and mysterious ancient civilisations make South America a more likely candidate than India as the place where the Aztec calendar clock was made. In this case, however, the date goes back prior to the end of Pleistocene, when the elephants disappeared from South America. It’s the same epoch when, according to Plato, Atlantis existed, the land of the “gods” par excellence, which in Plato’s account was swarming with elephants, to the point that if we would imagine a mark for it, the one represented on the sun stone would look the most appropriate and evocative. The mechanical clock reproduced on the sun stone by an unknown Aztec artist was the product of that civilisation, made with precious materials capable to last for the time that it was intended to measure: millennia.
Atlantis should be the mysterious ancient civilisation that for the first time measured the length of the synodic year with almost absolute precision and established those units of time from which calendars and numerical system of the ancient world were derived, still in use today.
- back: "home"
- Initial page
- Buy a book


